Take a look at the below equation. The answer is correct, so what is the problem with this?
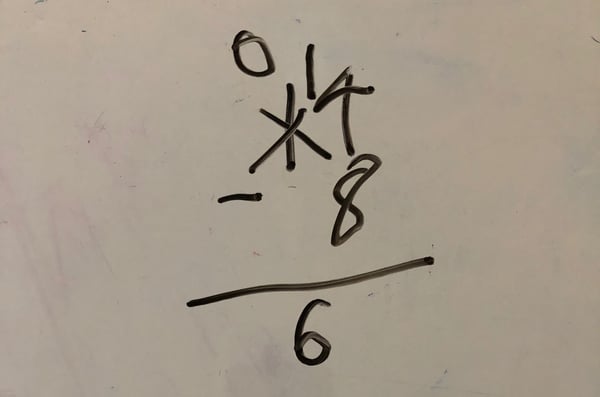
In mathematics, we often equate success with speed. The student who arrives at the answer quickly gets the gold star. But all too often, the student who is the fastest is representing a shallow understanding or an ability to memorize rather than conceptualize the mathematics.
Take for example, the above problem. The student who worked on this had clearly memorized a series of steps, or an algorithm to achieve success, but you can see that there is a lack of understanding of the concept behind the algorithm. If the student had understood how the numbers related to each other, they would have no need for the standard algorithm of "going next door to borrow" or regrouping. We need to move beyond memorizing algorithms and move toward a deeper understanding of mathematical concepts so that students understand how numbers relate to each other.
In mathematics, we often equate success with speed. The student who arrives at the answer quickly gets the gold star. But all too often, the student who is the fastest is representing a shallow understanding or an ability to memorize rather than conceptualize the mathematics.
We talk about fluency in mathematics — but what does that mean? The student who is fluent in mathematics is the student who demonstrates accuracy, efficiency, and flexibility. This is the student who can build upon prior knowledge and then strategize to see multiple pathways to a single problem. Sure this student may take more time to find the answer, but in the end, their understanding is much deeper. We need to show the same patience with our math students that we do with our readers. If a student speed reads through a text, we ask them to slow down, to think about the words they are reading, and to reflect on the author's message. So why then, do we push speed with math rather than nurturing the same understanding of number relationships?
Think about all the iPad apps and computer games that are designed to help students increase their math skills. The majority of them have a timer embedded and ask the student to complete a given set in a specific amount of time in order to achieve success. Why is it important how quickly you can solve the problem? In the elementary years, as students are developing their mathematical mindsets and are just beginning to view themselves as mathematicians, it is important to give them the space and the time to develop their strategies, to focus on their thinking, and to reflect on how numbers relate to each other. Slowing down at this stage, diving into the intricacies of numbers, and communicating about their strategies with each other, will inevitably allow them to develop a deep sense of understanding. This will in turn allow them to speed up and become more automatic as they continue on their math trajectory.
We need to give our math students the same opportunity to explore, inquire, communicate, make connections to prior learning and reflect that we do in our other subjects. Math is a language in and of itself and it takes time to build understanding. Students need to be made aware that they can build upon prior knowledge to make new connections and therefore build understanding for higher level concepts. Students will become more efficient, accurate, and flexible when they have time to reflect on their thinking and communicate with each other about different strategies and which to use in certain situations, thus developing and deepening their understandings.
Giving students time to collaborate and communicate with each other will yield results like these below. Students who can solve this problem in five, six, or 10 different ways have a much deeper understanding of the concept of subtraction!
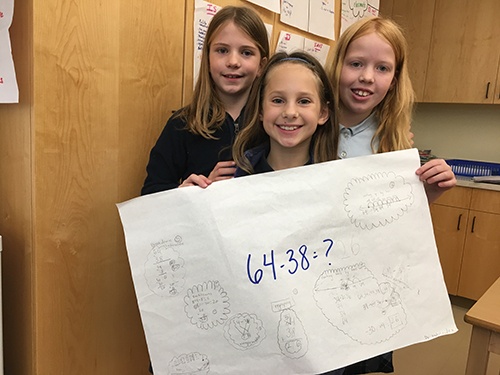
These students are building a tool kit from which they can draw upon for future situations. They are laying the foundation for algebra, calculus, and beyond by taking the time to inquire into the math, communicate their thinking, and reflect on the most efficient and effective strategy. These are students who will move beyond memorization and be able to apply their understanding to new and different situations. These are the mathematicians we want to foster.


